A graph is a mathematical concept which was first described in 1736 by Euler.
Starting at the beginning means explaining what a graph is. The picture in your head should look like this:
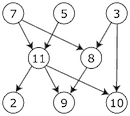
The graph is a directed (the arrowheads) and acyclic (no recursive loops) graph.
What graphs do very well is represent connected data.
Representing the real world is about communicating these two perspectives:
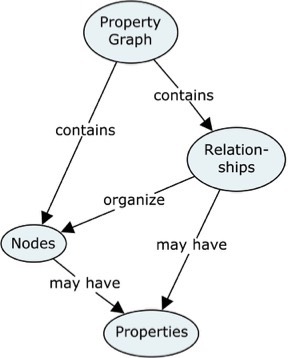
So, even if your physical target is not a graph database, borrowing the paradigms of the (property) graph to make platform-independent representations of data models makes perfect sense.
The concept map explains the most important concepts used in the property graph context:
Both Nodes and Relationships can (should) have “names” (formally called labels for nodes and types for relationships).
Relationships are directed, which is visualized by the arrowheads.
Both Nodes and Relationships may be associated with Properties, which are “key/value” pairs such as e.g. "Color/Red".
On the data model level, we call the key "Property Name".
The concept is used in computer science as a data structure, composed of nodes connected by edges.
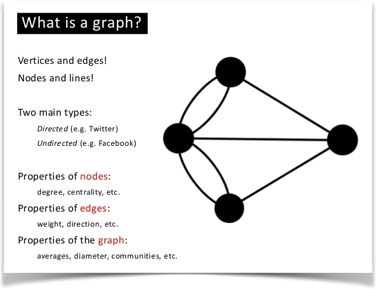
Each node represents some sort of entity, and each edge a relationship between two of those entities. Each edge may also have a direction and can store data. Social networks, such as Facebook, LinkedIn or Yammer, use this kind of data structure to represent the relationships between the people and the contents stored in it.
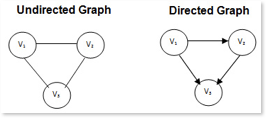
A directed graph (or digraph) is a set of vertices and a collection of directed edges that each connects an ordered pair of vertices.
We say that a directed edge points from the first vertex in the pair and points to the second vertex in the pair.
A graph is nothing more than an entity-relationship-sketch without technical tricks.

A graph can be easily rotated to provide an understandable access structure of the information. Applications and user experiences are setups this way. Boxary makes this explicit. Instead of targeting tables, matching where rules, the notation allows for specifying a path, matching attributes (compare pathfinders) and specifying the attributes to retrieve. To add intelligence a ''Lexicon' is provided.
Property graphs are mathematically well-founded by graph theory. Just as the relational model (Codd style) is based on mathematics by set theory.
Some rules must be considered:
A planar contains vertices and edges that constitute a particular model, which is used by the application. In general, one could say that a Planar can be drawn on a planar, i.e. in 2D.